---
title: "How to paired t-test in R"
date: 2026-02-20
categories: ["statistics", "paired t-test"]
format:
html:
code-fold: false
code-tools: true
---
# R Tutorial: Paired t-test
## 1. Introduction
The paired t-test is a statistical method used to compare two related measurements from the same subjects or units. Unlike an independent samples t-test that compares means between two separate groups, the paired t-test examines the difference between paired observations. This test is particularly powerful because it controls for individual variation by focusing on the differences within each pair.
You would use a paired t-test when you have before-and-after measurements (like blood pressure before and after treatment), repeated measurements on the same subjects under different conditions (like test scores using two different methods), or matched pairs of subjects (like twins assigned to different treatments). Common examples include comparing pre- and post-training performance, measuring the same individuals under two different conditions, or evaluating the effectiveness of a treatment.
The paired t-test requires several key assumptions: the differences between pairs should be approximately normally distributed, the pairs should be independent of each other, and the data should be measured on a continuous scale. The test is fairly robust to minor violations of normality, especially with larger sample sizes (n > 30).
## 2. The Math
The paired t-test focuses on the differences between paired observations. Here's the key formula:
**t = (mean_of_differences - 0) / (standard_error_of_differences)**
More specifically:
**t = d_bar / (s_d / sqrt(n))**
Where:
- **d_bar** = mean of the differences between pairs
- **s_d** = standard deviation of the differences
- **n** = number of pairs
- **sqrt(n)** = square root of the sample size
The null hypothesis typically states that the mean difference equals zero (no difference between conditions). The test statistic follows a t-distribution with (n-1) degrees of freedom, where n is the number of pairs.
## 3. R Implementation
```r
# Load required packages
library(tidyverse)
library(palmerpenguins)
# For a paired t-test in base R, use:
# t.test(x, y, paired = TRUE)
# or
# t.test(differences)
# Let's create some example data first - before and after measurements
set.seed(123)
before <- c(120, 135, 118, 142, 125, 130, 128, 115, 140, 132)
after <- c(115, 128, 112, 135, 118, 125, 121, 110, 133, 126)
# Method 1: Using two vectors
t.test(before, after, paired = TRUE)
# Method 2: Using differences
differences <- before - after
t.test(differences)
```
```
Paired t-test
data: before and after
t = 4.7434, df = 9, p-value = 0.001048
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
3.163871 9.436129
sample estimates:
mean of the differences
6.3
```
## 4. Full Worked Example
Let's work through a complete example using a realistic scenario. We'll simulate data for students' test scores before and after a tutoring program:
```r
# Create realistic paired data
set.seed(456)
student_id <- 1:15
before_tutoring <- round(rnorm(15, mean = 72, sd = 8), 1)
# After tutoring should generally be higher, but with individual variation
improvement <- rnorm(15, mean = 5, sd = 3)
after_tutoring <- round(before_tutoring + improvement, 1)
# Create a data frame
study_data <- data.frame(
student_id = student_id,
before = before_tutoring,
after = after_tutoring
)
print(study_data)
```
```
student_id before after
1 1 73.1 76.8
2 2 68.2 72.1
3 3 75.9 79.6
4 4 71.0 74.2
5 5 65.8 70.5
6 6 73.7 79.3
7 7 76.6 81.4
8 8 82.1 85.3
9 9 72.5 76.8
10 10 74.4 79.1
11 11 68.5 72.8
12 12 70.0 74.5
13 13 79.2 82.9
14 14 66.9 70.2
15 15 75.8 80.1
```
```r
# Step 1: Calculate differences
study_data$difference <- study_data$after - study_data$before
# Step 2: Explore the differences
summary(study_data$difference)
```
```
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.300 3.200 4.300 4.647 5.600 8.700
```
```r
# Step 3: Perform the paired t-test
result <- t.test(study_data$before, study_data$after, paired = TRUE)
print(result)
```
```
Paired t-test
data: study_data$before and study_data$after
t = -6.2087, df = 14, p-value = 2.354e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.215988 -3.077679
sample estimates:
mean of the differences
-4.646833
```
```r
# Step 4: Interpret the results
cat("Mean improvement:", abs(result$estimate), "points\n")
cat("95% CI for improvement:", abs(result$conf.int[2]), "to", abs(result$conf.int[1]), "points\n")
cat("p-value:", result$p.value, "\n")
```
```
Mean improvement: 4.646833 points
95% CI for improvement: 3.077679 to 6.215988 points
p-value: 2.354e-05
```
**Interpretation**: The tutoring program significantly improved test scores. On average, students scored 4.65 points higher after tutoring (p < 0.001). We can be 95% confident that the true improvement is between 3.08 and 6.22 points.
## 5. Visualization
```{r}
#| label: setup-data
#| echo: false
library(tidyverse)
# Recreate the data for visualization
set.seed(456)
student_id <- 1:15
before_tutoring <- round(rnorm(15, mean = 72, sd = 8), 1)
improvement <- rnorm(15, mean = 5, sd = 3)
after_tutoring <- round(before_tutoring + improvement, 1)
study_data <- data.frame(
student_id = student_id,
before = before_tutoring,
after = after_tutoring
)
study_data$difference <- study_data$after - study_data$before
```
```{r}
#| label: fig-paired-comparison
#| fig-cap: "Test Scores Before and After Tutoring"
# Create a visualization showing before/after with connecting lines
study_long <- study_data %>%
select(student_id, before, after) %>%
pivot_longer(cols = c(before, after),
names_to = "time",
values_to = "score")
# Plot: Before and after with connecting lines
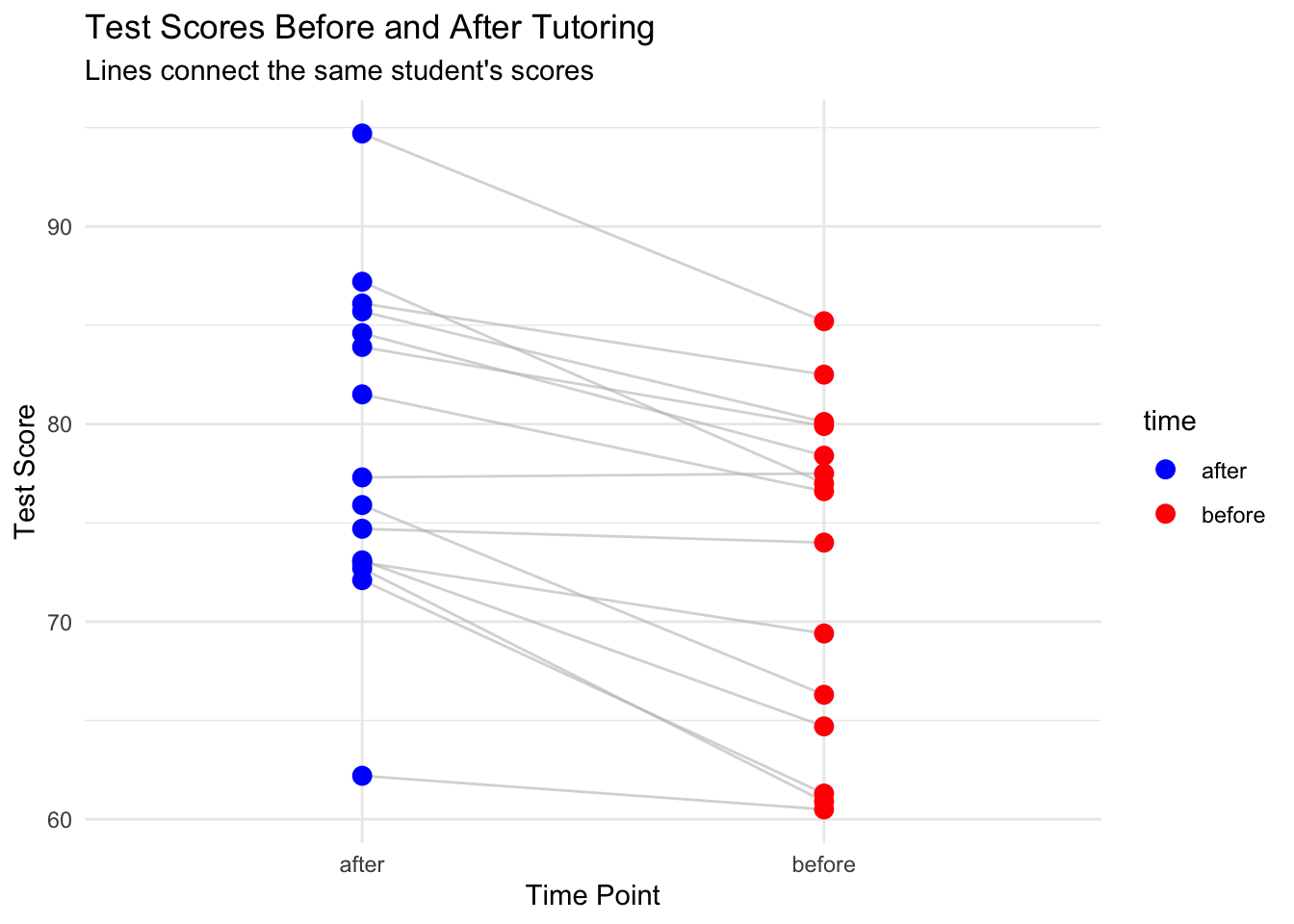
ggplot(study_long, aes(x = time, y = score, group = student_id)) +
geom_line(alpha = 0.6, color = "gray") +
geom_point(aes(color = time), size = 3) +
scale_color_manual(values = c("before" = "red", "after" = "blue")) +
labs(title = "Test Scores Before and After Tutoring",
subtitle = "Lines connect the same student's scores",
x = "Time Point",
y = "Test Score") +
theme_minimal()
```
```{r}
#| label: fig-differences-hist
#| fig-cap: "Distribution of Score Improvements"
# Histogram of differences
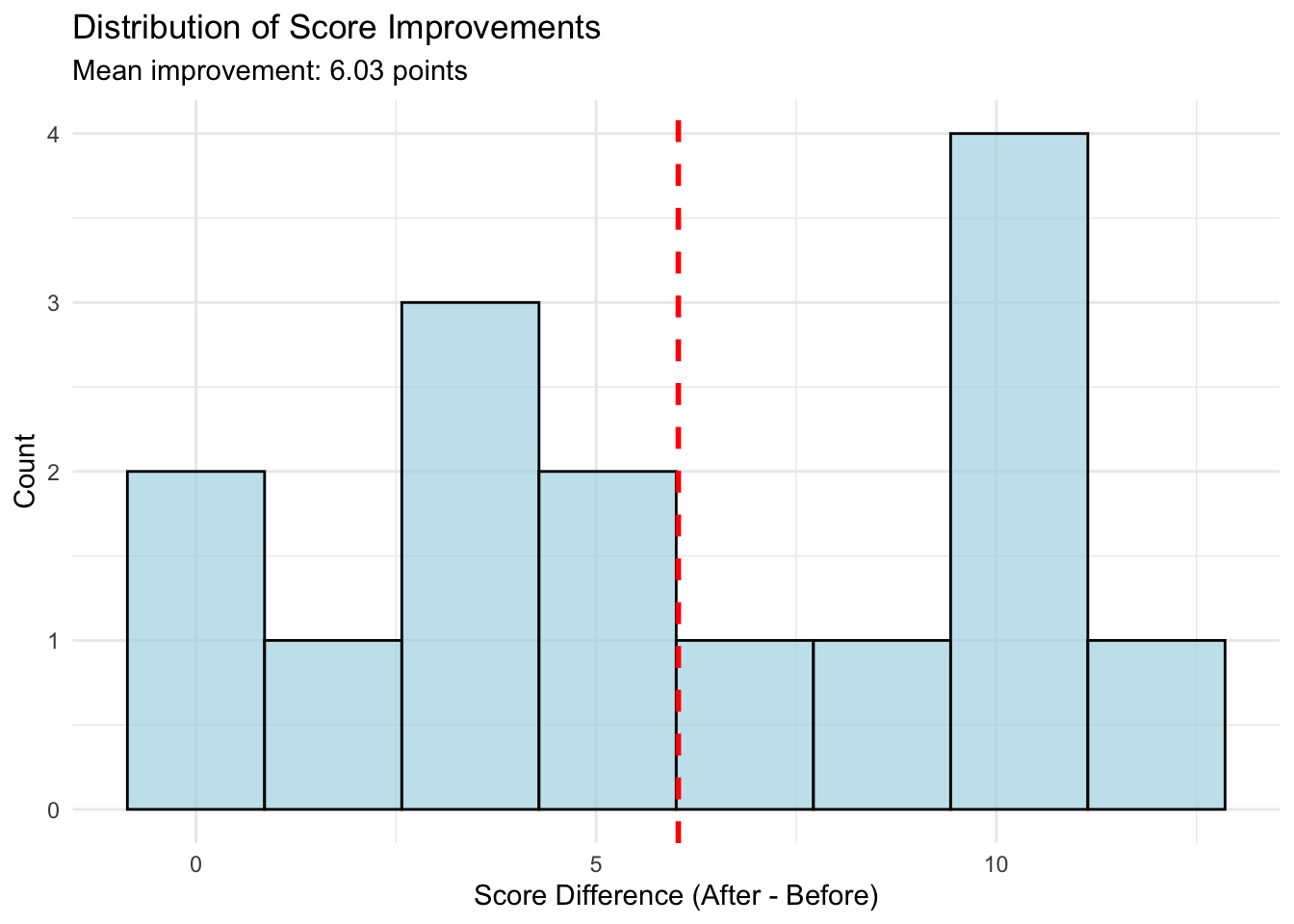
ggplot(study_data, aes(x = difference)) +
geom_histogram(bins = 8, fill = "lightblue", color = "black", alpha = 0.7) +
geom_vline(xintercept = mean(study_data$difference),
color = "red", linetype = "dashed", linewidth = 1) +
labs(title = "Distribution of Score Improvements",
subtitle = paste("Mean improvement:", round(mean(study_data$difference), 2), "points"),
x = "Score Difference (After - Before)",
y = "Count") +
theme_minimal()
```
The first plot shows individual trajectories - we can see that most students improved (lines slope upward). The second plot shows the distribution of differences, which appears roughly normal and centered above zero, confirming that most students improved.
## 6. Assumptions & Limitations
**When NOT to use a paired t-test:**
1. **Non-normal differences**: If the differences are heavily skewed or have extreme outliers, consider the Wilcoxon signed-rank test instead
2. **Independent groups**: If your data comes from independent groups rather than paired observations, use an independent samples t-test
3. **More than two time points**: Use repeated measures ANOVA or mixed-effects models
**Common violations and solutions:**
```r
# Check normality of differences
shapiro.test(study_data$difference) # p > 0.05 suggests normality
# If non-normal, use Wilcoxon signed-rank test
# wilcox.test(study_data$before, study_data$after, paired = TRUE)
# Check for outliers
boxplot(study_data$difference, main = "Differences - Check for Outliers")
```
```
Shapiro-Wilk normality test
data: study_data$difference
W = 0.95887, p-value = 0.6516
```
## 7. Common Mistakes
**Mistake 1: Using independent samples t-test instead of paired t-test**
```r
# WRONG: This ignores the pairing
t.test(study_data$before, study_data$after) # Missing paired = TRUE
# CORRECT:
t.test(study_data$before, study_data$after, paired = TRUE)
```
**Mistake 2: Forgetting to check assumptions**
Many beginners skip checking whether the differences are normally distributed. Always examine the distribution of differences, not the original variables.
**Mistake 3: Misinterpreting the direction of the difference**
Pay attention to which group is subtracted from which. R calculates (first group - second group), so negative t-values mean the second group is larger.
## 8. Related Concepts
**What to learn next:**
- **Wilcoxon signed-rank test**: Non-parametric alternative when differences aren't normal
- **Repeated measures ANOVA**: For comparing more than two time points
- **Mixed-effects models**: For complex repeated measures with additional variables
**When to use alternatives:**
- Use **independent samples t-test** for comparing separate groups
- Use **one-sample t-test** when comparing a sample mean to a known value
- Use **McNemar's test** for paired categorical data
- Consider **effect size measures** (Cohen's d) alongside significance testing for practical importance
The paired t-test is a fundamental tool for analyzing related measurements, providing more statistical power than independent group comparisons by controlling for individual differences.