---
title: "How to t-test for two samples in R"
date: 2026-02-20
categories: ["statistics", "t-test for two samples"]
format:
html:
code-fold: false
code-tools: true
---
# Two-Sample t-test in R: A Comprehensive Tutorial
## 1. Introduction
The two-sample t-test is a fundamental statistical test used to compare the means of two independent groups to determine if they differ significantly. For example, you might want to compare the average heights of male and female penguins, or test whether two different teaching methods produce different test scores.
This test helps answer questions like: "Is the difference I observe between these two groups likely due to chance, or does it represent a real difference in the population?" The two-sample t-test is appropriate when you have continuous data from two independent groups and want to compare their means.
The test requires several key assumptions: the data should be approximately normally distributed within each group, the observations should be independent, and ideally, the variances of the two groups should be similar (homoscedasticity). When these assumptions are met, the t-test provides a robust method for comparing group means.
The output gives you a t-statistic and p-value, helping you decide whether to reject the null hypothesis that the two group means are equal. This makes it an essential tool for experimental research, quality control, and data analysis across many fields.
## 2. The Math
The two-sample t-test formula depends on whether you assume equal or unequal variances between groups.
**For equal variances (pooled t-test):**
```
t = (x̄₁ - x̄₂) / (sp × √(1/n₁ + 1/n₂))
```
**For unequal variances (Welch's t-test):**
```
t = (x̄₁ - x̄₂) / √(s₁²/n₁ + s₂²/n₂)
```
Where:
- x̄₁ and x̄₂ = sample means of groups 1 and 2
- s₁² and s₂² = sample variances of groups 1 and 2
- n₁ and n₂ = sample sizes of groups 1 and 2
- sp = pooled standard deviation = √[((n₁-1)s₁² + (n₂-1)s₂²) / (n₁+n₂-2)]
The t-statistic measures how many standard errors the difference in means is away from zero. A larger absolute t-value suggests a more significant difference between groups.
## 3. R Implementation
Let's explore how to perform two-sample t-tests in R using the palmerpenguins dataset:
```r
# Load required packages
library(tidyverse)
library(palmerpenguins)
# Load and explore the data
data(penguins)
head(penguins)
```
```
# A tibble: 6 × 8
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
<fct> <fct> <dbl> <dbl> <int> <int>
1 Adelie Torgersen 39.1 18.7 181 3750
2 Adelie Torgersen 39.5 17.4 186 3800
3 Adelie Torgersen 40.3 18 195 3250
4 Adelie Torgersen NA NA NA NA
5 Adelie Torgersen 36.7 19.3 193 3450
6 Adelie Torgersen 39.3 20.6 190 3650
# … with 2 more variables: sex <fct>, year <int>
```
**Basic t-test syntax in R:**
```r
# Method 1: Using formula syntax
t.test(bill_length_mm ~ sex, data = penguins)
# Method 2: Using separate vectors
male_bills <- penguins$bill_length_mm[penguins$sex == "male"]
female_bills <- penguins$bill_length_mm[penguins$sex == "female"]
t.test(male_bills, female_bills)
# Method 3: Using tidyverse approach
penguins %>%
filter(!is.na(sex), !is.na(bill_length_mm)) %>%
t.test(bill_length_mm ~ sex, data = .)
```
## 4. Full Worked Example
Let's compare bill lengths between male and female penguins step by step:
```r
# Step 1: Clean and prepare the data
penguins_clean <- penguins %>%
filter(!is.na(sex), !is.na(bill_length_mm))
# Step 2: Explore the data
penguins_clean %>%
group_by(sex) %>%
summarise(
count = n(),
mean_bill = mean(bill_length_mm),
sd_bill = sd(bill_length_mm),
.groups = 'drop'
)
```
```
# A tibble: 2 × 4
sex count mean_bill sd_bill
<fct> <int> <dbl> <dbl>
1 female 165 42.1 4.90
2 male 168 45.9 5.37
```
```r
# Step 3: Perform the t-test
t_test_result <- t.test(bill_length_mm ~ sex,
data = penguins_clean,
var.equal = FALSE) # Welch's t-test
print(t_test_result)
```
```
Welch Two Sample t-test
data: bill_length_mm by sex
t = -6.4966, df = 328.05, p-value = 3.564e-10
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
-4.874190 -2.555544
sample estimates:
mean in group female mean in group male
42.09685 45.81190
```
**Interpretation:**
- The t-statistic is -6.497, indicating male penguins have significantly longer bills
- The p-value (3.564e-10) is much smaller than 0.05, so we reject the null hypothesis
- The 95% confidence interval for the difference is (-4.87, -2.56) mm
- Male penguins have bills that are, on average, 3.71 mm longer than females
## 5. Visualization
```{r}
#| label: setup-ttest-data
#| echo: false
library(tidyverse)
library(palmerpenguins)
penguins_clean <- penguins %>%
filter(!is.na(sex), !is.na(bill_length_mm))
```
```{r}
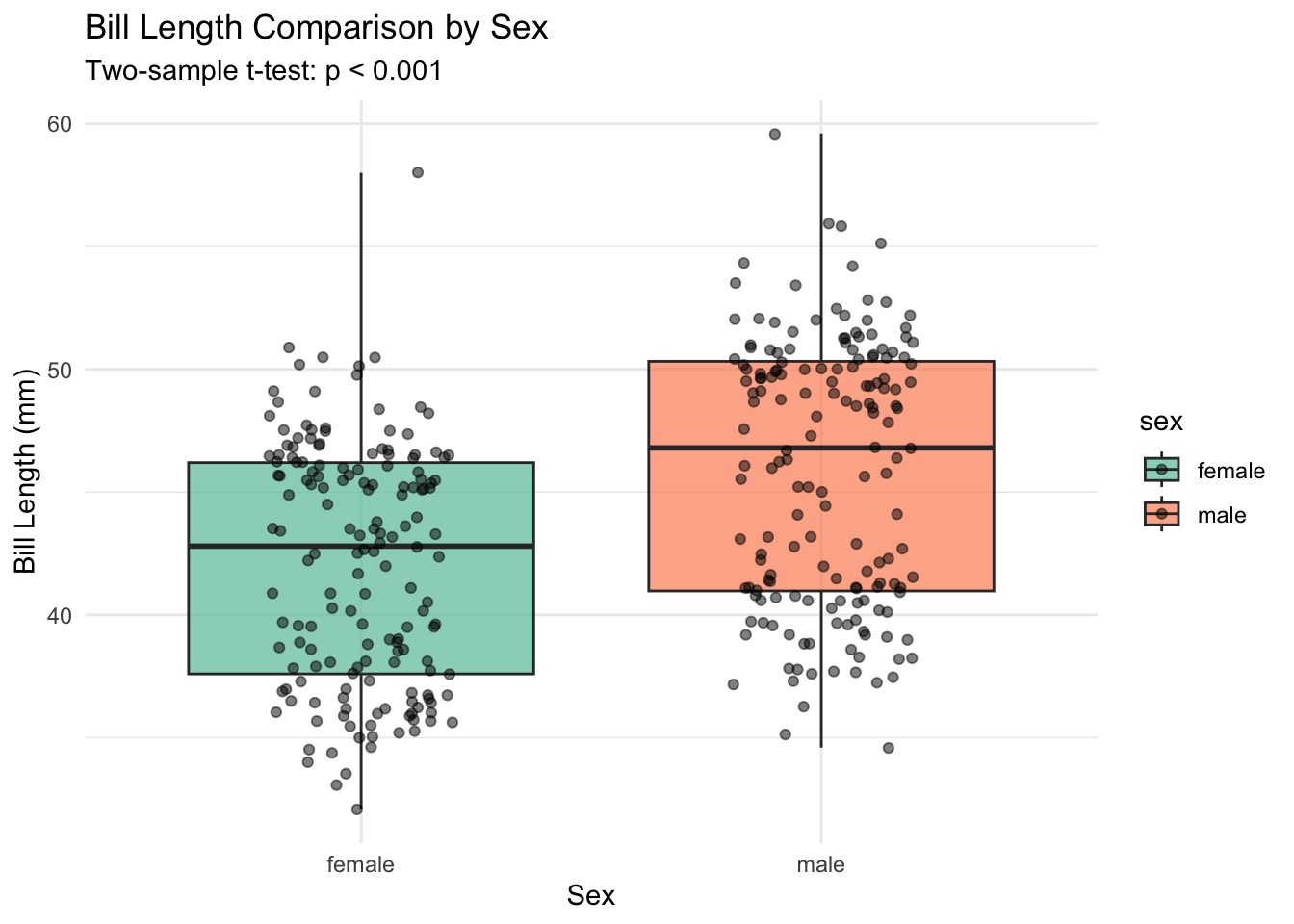
#| label: fig-boxplot-sex
#| fig-cap: "Bill Length Comparison by Sex"
# Create a visualization comparing the two groups
penguins_clean %>%
ggplot(aes(x = sex, y = bill_length_mm, fill = sex)) +
geom_boxplot(alpha = 0.7) +
geom_jitter(width = 0.2, alpha = 0.5) +
labs(
title = "Bill Length Comparison by Sex",
subtitle = "Two-sample t-test: p < 0.001",
x = "Sex",
y = "Bill Length (mm)"
) +
theme_minimal() +
scale_fill_brewer(palette = "Set2")
```
```{r}
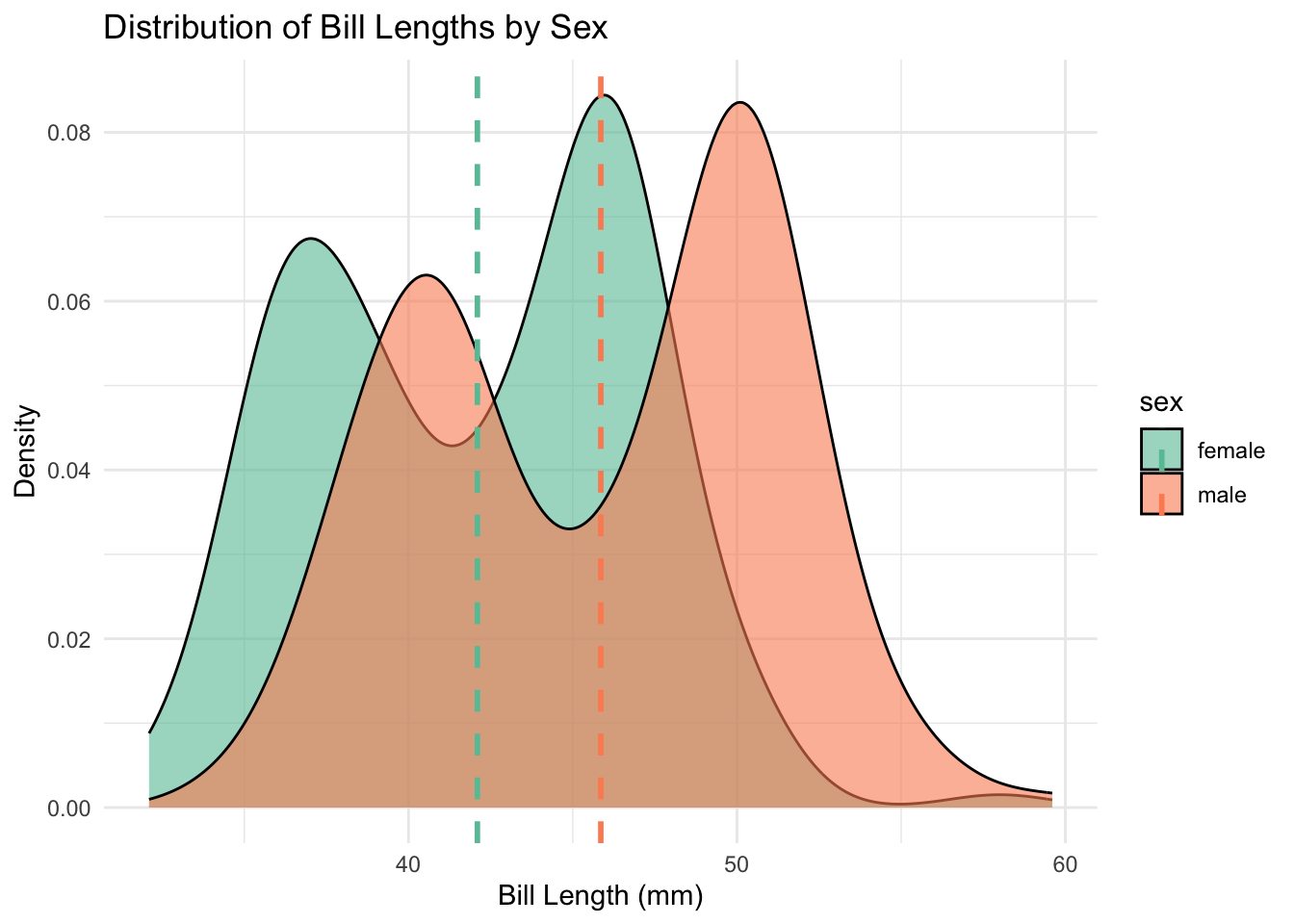
#| label: fig-density-sex
#| fig-cap: "Distribution of Bill Lengths by Sex"
# Density plot for better comparison
penguins_clean %>%
ggplot(aes(x = bill_length_mm, fill = sex)) +
geom_density(alpha = 0.6) +
geom_vline(data = penguins_clean %>% group_by(sex) %>%
summarise(mean_bill = mean(bill_length_mm), .groups = "drop"),
aes(xintercept = mean_bill, color = sex),
linetype = "dashed", linewidth = 1) +
labs(
title = "Distribution of Bill Lengths by Sex",
x = "Bill Length (mm)",
y = "Density"
) +
theme_minimal() +
scale_fill_brewer(palette = "Set2") +
scale_color_brewer(palette = "Set2")
```
These plots show clear separation between the two groups, with males having consistently longer bills. The boxplot reveals the medians, quartiles, and outliers, while the density plot shows the shape of each distribution and highlights the difference in means with dashed lines.
## 6. Assumptions & Limitations
**Key Assumptions:**
1. **Independence**: Observations within and between groups must be independent
2. **Normality**: Data should be approximately normally distributed within each group
3. **Homogeneity of variance**: Groups should have similar variances (for pooled t-test)
**When NOT to use two-sample t-test:**
```r
# Check normality with Shapiro-Wilk test
penguins_clean %>%
group_by(sex) %>%
summarise(
shapiro_p = shapiro.test(bill_length_mm)$p.value,
.groups = 'drop'
)
```
```
# A tibble: 2 × 2
sex shapiro_p
<fct> <dbl>
1 female 0.454
2 male 0.719
```
**Alternatives when assumptions are violated:**
- **Non-normal data**: Use Mann-Whitney U test (Wilcoxon rank-sum test)
- **Unequal variances**: Use Welch's t-test (default in R)
- **Paired data**: Use paired t-test instead
- **Multiple groups**: Use ANOVA
```r
# Example: Non-parametric alternative
wilcox.test(bill_length_mm ~ sex, data = penguins_clean)
```
## 7. Common Mistakes
**Mistake 1: Using paired t-test for independent samples**
```r
# WRONG: Don't use paired=TRUE for independent groups
t.test(bill_length_mm ~ sex, data = penguins_clean, paired = TRUE)
# CORRECT: Use independent samples t-test
t.test(bill_length_mm ~ sex, data = penguins_clean)
```
**Mistake 2: Ignoring missing values**
```r
# WRONG: Not handling NAs can cause errors
t.test(bill_length_mm ~ sex, data = penguins) # May cause issues
# CORRECT: Remove NAs first
t.test(bill_length_mm ~ sex,
data = penguins %>% filter(!is.na(sex), !is.na(bill_length_mm)))
```
**Mistake 3: Misinterpreting p-values**
A p-value of 0.03 doesn't mean there's a 97% chance the groups are different. It means that if there were no true difference, you'd see a difference this large or larger 3% of the time by chance alone.
## 8. Related Concepts
**What to learn next:**
- **One-way ANOVA**: For comparing means across multiple groups
- **Paired t-test**: For comparing the same subjects under two conditions
- **Effect size calculations**: Cohen's d for practical significance
- **Power analysis**: Determining appropriate sample sizes
**When to use alternatives:**
- **Mann-Whitney U test**: When data isn't normally distributed
- **Bootstrap methods**: For robust inference without distributional assumptions
- **Bayesian t-tests**: When you want to incorporate prior information
```r
# Quick example of effect size (Cohen's d)
library(effsize)
cohen.d(bill_length_mm ~ sex, data = penguins_clean)
```
The two-sample t-test is your gateway to understanding group comparisons in statistics. Master this concept, and you'll be well-prepared for more advanced statistical techniques!