---
title: "How to z-score normalization in R"
date: 2026-02-20
categories: ["statistics", "z-score normalization"]
format:
html:
code-fold: false
code-tools: true
---
# Z-Score Normalization in R: A Complete Tutorial
## 1. Introduction
Z-score normalization, also known as standardization, is a statistical technique that transforms data to have a mean of 0 and a standard deviation of 1. This process converts raw data points into z-scores, which represent how many standard deviations a value is from the mean.
You would use z-score normalization when you need to compare variables measured on different scales, prepare data for machine learning algorithms that are sensitive to scale (like PCA or clustering), or identify outliers in your data. It's particularly useful when combining multiple variables into a single analysis or when you want to understand where individual observations stand relative to the group.
Z-score normalization assumes that your data follows a roughly normal distribution for optimal interpretation, though the mathematical transformation works on any distribution. The technique also assumes that the mean and standard deviation are meaningful measures for your data, which means extreme outliers can significantly affect the results. While the transformation itself doesn't require perfectly normal data, interpreting z-scores in terms of probability and percentiles works best when the underlying distribution is approximately normal.
## 2. The Math
The formula for calculating a z-score is straightforward:
**z = (x - mean) / standard_deviation**
Where:
- **z** = the z-score (standardized value)
- **x** = the original data value
- **mean** = the arithmetic mean of all values in the dataset
- **standard_deviation** = the standard deviation of all values in the dataset
For a sample standard deviation (which we typically use), the formula becomes:
**z = (x - x̄) / s**
Where x̄ represents the sample mean and s represents the sample standard deviation. After transformation, the new dataset will have a mean of exactly 0 and a standard deviation of exactly 1, regardless of the original scale of measurement.
## 3. R Implementation
Let's start by loading the necessary packages and exploring our data:
```r
library(tidyverse)
library(palmerpenguins)
# Look at the penguins dataset
head(penguins)
```
```
# A tibble: 6 × 8
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
<fct> <fct> <dbl> <dbl> <int> <int>
1 Adelie Torgersen 39.1 18.7 181 3750
2 Adelie Torgersen 39.5 17.4 186 3800
3 Adelie Torgersen 40.3 18 195 4050
4 Adelie Torgersen NA NA NA NA
5 Adelie Torgersen 36.7 19.3 193 3450
6 Adelie Torgersen 39.3 20.6 190 3650
# ℹ 2 more variables: sex <fct>, year <int>
```
Here are three ways to perform z-score normalization in R:
**Method 1: Base R function**
```r
# Using the scale() function
penguins_clean <- penguins %>% drop_na()
bill_length_z <- scale(penguins_clean$bill_length_mm)
head(bill_length_z)
```
```
[,1]
[1,] -0.8832047
[2,] -0.8099821
[3,] -0.6635369
[4,] -1.3229897
[5,] -0.8465934
[6,] -0.9198160
```
**Method 2: Manual calculation**
```r
# Manual z-score calculation
manual_z <- (penguins_clean$bill_length_mm - mean(penguins_clean$bill_length_mm)) /
sd(penguins_clean$bill_length_mm)
head(manual_z)
```
```
[1] -0.8832047 -0.8099821 -0.6635369 -1.3229897 -0.8465934 -0.9198160
```
**Method 3: Tidyverse approach**
```r
# Using dplyr for multiple columns
penguins_normalized <- penguins_clean %>%
mutate(
bill_length_z = scale(bill_length_mm)[,1],
bill_depth_z = scale(bill_depth_mm)[,1],
flipper_length_z = scale(flipper_length_mm)[,1],
body_mass_z = scale(body_mass_g)[,1]
)
```
## 4. Full Worked Example
Let's work through a complete example using penguin bill length:
```r
# Step 1: Prepare the data
penguins_clean <- penguins %>%
drop_na(bill_length_mm)
# Step 2: Calculate original statistics
original_mean <- mean(penguins_clean$bill_length_mm)
original_sd <- sd(penguins_clean$bill_length_mm)
cat("Original mean:", round(original_mean, 2), "mm\n")
cat("Original standard deviation:", round(original_sd, 2), "mm\n")
```
```
Original mean: 43.92 mm
Original standard deviation: 5.46 mm
```
```r
# Step 3: Apply z-score normalization
penguins_clean$bill_length_z <- scale(penguins_clean$bill_length_mm)[,1]
# Step 4: Verify the transformation
new_mean <- mean(penguins_clean$bill_length_z)
new_sd <- sd(penguins_clean$bill_length_z)
cat("Normalized mean:", round(new_mean, 10), "\n")
cat("Normalized standard deviation:", round(new_sd, 2), "\n")
```
```
Normalized mean: 0
Normalized standard deviation: 1
```
```r
# Step 5: Compare some original vs normalized values
comparison <- penguins_clean %>%
select(species, bill_length_mm, bill_length_z) %>%
slice_head(n = 8)
print(comparison)
```
```
# A tibble: 8 × 3
species bill_length_mm bill_length_z
<fct> <dbl> <dbl>
1 Adelie 39.1 -0.883
2 Adelie 39.5 -0.810
3 Adelie 40.3 -0.664
4 Adelie 36.7 -1.32
5 Adelie 39.3 -0.847
6 Adelie 39.3 -0.847
7 Adelie 38.9 -0.920
8 Adelie 39.2 -0.865
```
**Interpretation**: The z-scores tell us how many standard deviations each penguin's bill length is from the average. For example, the first penguin has a bill length of 39.1mm, which is about 0.88 standard deviations below the average bill length across all penguins.
## 5. Visualization
Let's create visualizations to show the effect of z-score normalization:
```{r}
#| label: setup-zscore-data
#| echo: false
library(tidyverse)
library(palmerpenguins)
penguins_clean <- penguins %>% drop_na(bill_length_mm)
penguins_clean$bill_length_z <- scale(penguins_clean$bill_length_mm)[,1]
```
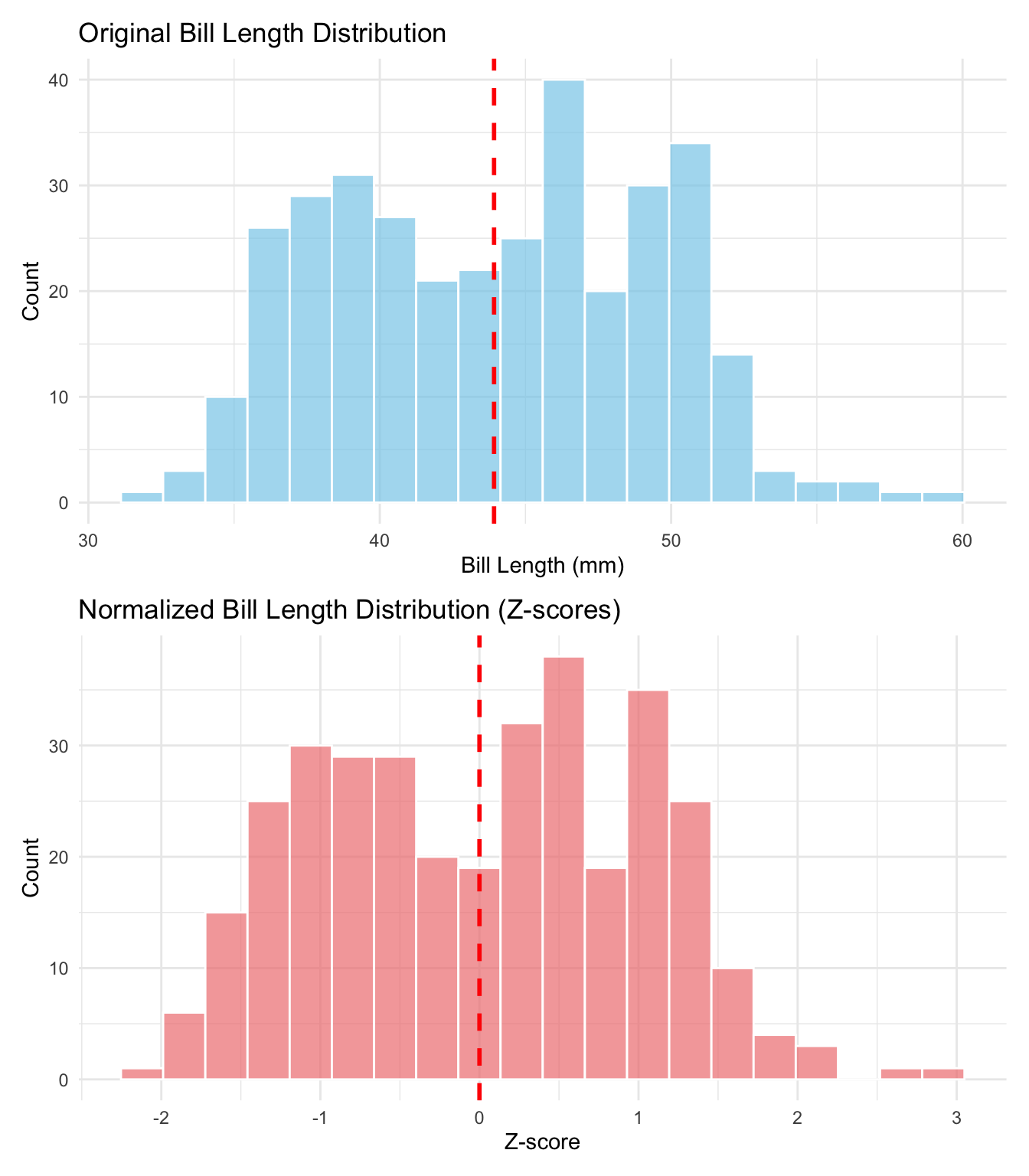
```{r}
#| label: fig-zscore-comparison
#| fig-cap: "Before and After Z-Score Normalization"
#| fig-height: 8
library(patchwork)
# Original distribution
p1 <- ggplot(penguins_clean, aes(x = bill_length_mm)) +
geom_histogram(bins = 20, fill = "skyblue", color = "white", alpha = 0.7) +
geom_vline(xintercept = mean(penguins_clean$bill_length_mm),
color = "red", linetype = "dashed", linewidth = 1) +
labs(title = "Original Bill Length Distribution",
x = "Bill Length (mm)",
y = "Count") +
theme_minimal()
# Normalized distribution
p2 <- ggplot(penguins_clean, aes(x = bill_length_z)) +
geom_histogram(bins = 20, fill = "lightcoral", color = "white", alpha = 0.7) +
geom_vline(xintercept = 0, color = "red", linetype = "dashed", linewidth = 1) +
labs(title = "Normalized Bill Length Distribution (Z-scores)",
x = "Z-score",
y = "Count") +
theme_minimal()
# Combine plots
p1 / p2
```
This visualization shows how z-score normalization preserves the shape of the distribution while centering it at 0 and scaling it to have a standard deviation of 1. The red dashed line shows the mean in each case - notice how it shifts from ~44mm to exactly 0.
## 6. Assumptions & Limitations
**When NOT to use z-score normalization:**
1. **With heavily skewed data**: Z-scores work best with roughly symmetric distributions. For highly skewed data, consider log transformation first or use robust scaling methods.
2. **When the standard deviation is very small or zero**: If your data has little variation, z-scores can create artificially large values or undefined results.
3. **With categorical or ordinal data**: Z-scores are meaningful only for continuous numerical data where mean and standard deviation make sense.
4. **When outliers are important**: Z-score normalization is sensitive to outliers, which can skew the mean and standard deviation, affecting the entire transformation.
```r
# Example of problematic case - data with outliers
problematic_data <- c(1, 2, 3, 4, 5, 100) # 100 is an outlier
z_scores <- scale(problematic_data)[,1]
print(z_scores)
```
```
[,1]
[1,] -0.6063391
[2,] -0.5819445
[3,] -0.5575499
[4,] -0.5331553
[5,] -0.5087607
[6,] 3.2877495
```
Notice how the outlier (100) dominates the transformation, making all other values appear very similar.
## 7. Common Mistakes
**Mistake 1: Normalizing data with missing values**
```r
# Wrong way - will produce errors
data_with_na <- c(1, 2, 3, NA, 5)
# scale(data_with_na) # This would cause issues
# Right way - handle missing values first
clean_data <- data_with_na[!is.na(data_with_na)]
scale(clean_data)
```
**Mistake 2: Assuming z-scores are percentiles**
Z-scores are not percentiles! A z-score of 1 doesn't mean the 100th percentile. Z-scores only correspond to percentiles when data is normally distributed.
**Mistake 3: Normalizing each group separately when you want to compare groups**
```r
# Wrong - normalizes within each species
penguins %>%
group_by(species) %>%
mutate(bill_length_z = scale(bill_length_mm)[,1])
# Right - normalizes across all species for comparison
penguins %>%
mutate(bill_length_z = scale(bill_length_mm)[,1])
```
## 8. Related Concepts
**What to learn next:**
- **Min-Max normalization**: Scales data to a specific range (usually 0-1), better when you know the theoretical bounds of your data
- **Robust scaling**: Uses median and interquartile range instead of mean and standard deviation, less sensitive to outliers
- **Quantile normalization**: Transforms data to follow a uniform distribution
**When to use alternatives:**
- Use **Min-Max scaling** when you need values in a specific range and your data doesn't have outliers
- Use **Robust scaling** when your data has outliers but you still want a standardization approach
- Use **Log transformation** followed by z-scoring for right-skewed data
- Consider **Rank transformation** for ordinal data or when you only care about relative ordering
Z-score normalization is a fundamental preprocessing step in data science, particularly useful for machine learning algorithms that assume features are on similar scales. Understanding when and how to apply it correctly will significantly improve your data analysis workflows.