---
title: "How to mean and median in R"
date: 2026-02-20
categories: ["statistics", "mean and median"]
format:
html:
code-fold: false
code-tools: true
---
# Understanding Mean and Median in R: A Complete Tutorial
## 1. Introduction
The **mean** and **median** are two fundamental measures of central tendency that help us understand the "typical" or "average" value in a dataset. The mean is the arithmetic average of all values, while the median is the middle value when data is arranged in order.
**When to use the mean:** The mean works best with normally distributed, continuous data without extreme outliers. It's ideal for calculating totals, averages for reporting, and when all data points should contribute equally to the central measure. Examples include average test scores, mean temperature, or average sales figures.
**When to use the median:** The median is preferred when data contains outliers, is skewed, or when you want a measure that represents the "typical" observation rather than the mathematical average. It's particularly useful for income data, house prices, or any dataset where extreme values might distort the mean.
**Key assumptions:** The mean assumes that extreme values are meaningful and should influence the central measure. The median assumes an ordinal relationship between values but is robust to outliers. Both require at least interval-level data, though median can work with ordinal data. Neither requires normal distribution, but the mean's interpretation is clearer with symmetric distributions.
## 2. The Math
**Mean Formula:**
```
Mean = (Sum of all values) / (Number of values)
Mean = (x₁ + x₂ + x₃ + ... + xₙ) / n
```
Where:
- x₁, x₂, x₃, ..., xₙ are individual data points
- n is the total number of observations
**Median Calculation:**
1. Sort all values from smallest to largest
2. If n is odd: Median = middle value
3. If n is even: Median = (middle two values) / 2
For example, with values [1, 3, 5, 7, 9], the median is 5 (middle value). With values [2, 4, 6, 8], the median is (4 + 6) / 2 = 5.
## 3. R Implementation
Let's start by loading necessary packages and exploring the basic functions:
```r
# Load required packages
library(tidyverse)
library(palmerpenguins)
# Basic mean and median functions
data <- c(10, 15, 20, 25, 30, 35, 100)
# Calculate mean
mean(data)
```
```
[1] 33.57143
```
```r
# Calculate median
median(data)
```
```
[1] 25
```
```r
# Handle missing values
data_with_na <- c(10, 15, NA, 25, 30)
mean(data_with_na, na.rm = TRUE)
```
```
[1] 20
```
```r
median(data_with_na, na.rm = TRUE)
```
```
[1] 20
```
Using tidyverse for grouped calculations:
```r
# Load penguins data
data(penguins)
# Calculate mean and median by species
penguins %>%
group_by(species) %>%
summarise(
mean_bill_length = mean(bill_length_mm, na.rm = TRUE),
median_bill_length = median(bill_length_mm, na.rm = TRUE),
.groups = 'drop'
)
```
```
# A tibble: 3 × 3
species mean_bill_length median_bill_length
<fct> <dbl> <dbl>
1 Adelie 38.8 38.8
2 Chinstrap 48.8 49.6
3 Gentoo 47.5 47.3
```
## 4. Full Worked Example
Let's analyze penguin body mass to understand the difference between mean and median:
```r
# Step 1: Explore the data
penguins %>%
select(species, body_mass_g) %>%
summary()
```
```
species body_mass_g
Adelie :152 Min. :2700
Chinstrap: 68 1st Qu.:3550
Gentoo :124 Median :4050
Mean :4202
3rd Qu.:4750
Max. :6300
NA's :2
```
```r
# Step 2: Calculate overall mean and median
overall_stats <- penguins %>%
summarise(
count = sum(!is.na(body_mass_g)),
mean_mass = mean(body_mass_g, na.rm = TRUE),
median_mass = median(body_mass_g, na.rm = TRUE),
difference = mean_mass - median_mass
)
overall_stats
```
```
# A tibble: 1 × 4
count mean_mass median_mass difference
<int> <dbl> <dbl> <dbl>
1 342 4202 4050 152
```
```r
# Step 3: Compare by species
species_stats <- penguins %>%
group_by(species) %>%
summarise(
count = sum(!is.na(body_mass_g)),
mean_mass = mean(body_mass_g, na.rm = TRUE),
median_mass = median(body_mass_g, na.rm = TRUE),
difference = mean_mass - median_mass,
.groups = 'drop'
)
species_stats
```
```
# A tibble: 3 × 5
species count mean_mass median_mass difference
<fct> <int> <dbl> <dbl> <dbl>
1 Adelie 151 3701 3700 0.7
2 Chinstrap 68 3733 3700 32.6
3 Gentoo 123 5076 5000 75.8
```
**Interpretation:** The overall mean (4202g) is higher than the median (4050g), suggesting a right-skewed distribution with some heavier penguins pulling the mean upward. Gentoo penguins show the largest difference between mean and median, indicating more variability or potential outliers in their body mass.
## 5. Visualization
```{r}
#| label: setup-mean-median
#| echo: false
library(tidyverse)
library(palmerpenguins)
```
```{r}
#| label: fig-mean-median
#| fig-cap: "Penguin Body Mass: Mean vs Median by Species"
# Calculate statistics for plotting
plot_data <- penguins %>%
filter(!is.na(body_mass_g)) %>%
group_by(species) %>%
summarise(
mean_mass = mean(body_mass_g),
median_mass = median(body_mass_g),
.groups = 'drop'
) %>%
pivot_longer(cols = c(mean_mass, median_mass),
names_to = "statistic", values_to = "value") %>%
mutate(statistic = case_when(
statistic == "mean_mass" ~ "Mean",
statistic == "median_mass" ~ "Median"
))
# Create the plot
ggplot(penguins %>% filter(!is.na(body_mass_g)),
aes(x = species, y = body_mass_g, fill = species)) +
geom_boxplot(alpha = 0.7) +
geom_point(data = plot_data, aes(x = species, y = value, shape = statistic),
size = 4, color = "black") +
scale_shape_manual(values = c("Mean" = 16, "Median" = 17)) +
labs(title = "Penguin Body Mass: Mean vs Median by Species",
subtitle = "Circles = Mean, Triangles = Median",
x = "Species", y = "Body Mass (g)",
shape = "Statistic") +
theme_minimal() +
theme(legend.position = "bottom")
```
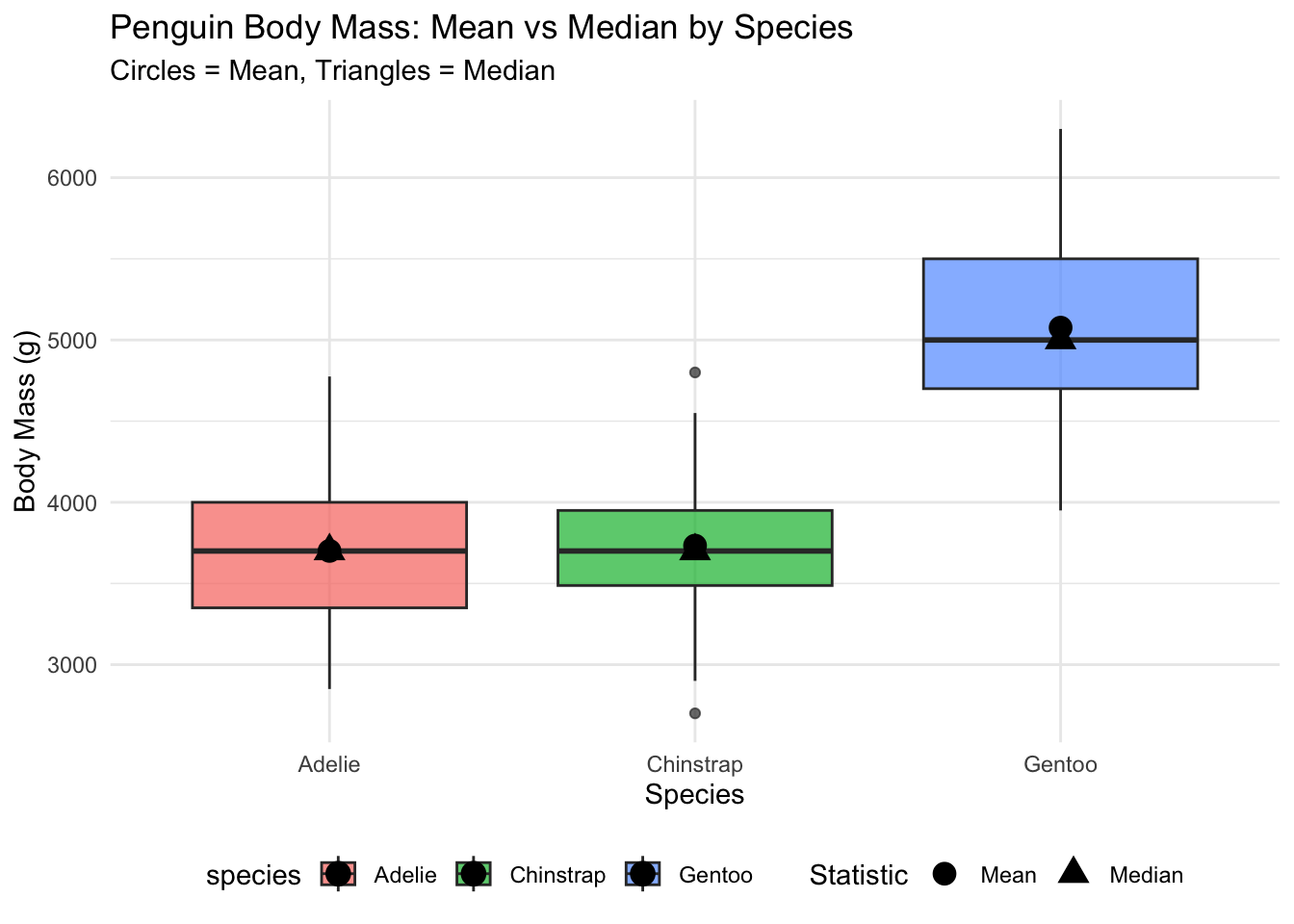
This plot shows the distribution of body mass for each penguin species with boxplots, overlaid with points showing the mean (circles) and median (triangles). Notice how the mean and median are nearly identical for Adelie penguins, suggesting a symmetric distribution, while Gentoo penguins show the mean above the median, indicating right skewness.
## 6. Assumptions & Limitations
**When NOT to use the mean:**
- With highly skewed data (income, real estate prices)
- When outliers significantly distort the central tendency
- With ordinal data where intervals aren't meaningful
- When you need a value that actually exists in your dataset
**When NOT to use the median:**
- When you need to account for the magnitude of all values
- For calculating totals or when extreme values are meaningful
- When working with small, symmetric datasets where mean is more precise
- In mathematical operations where additivity is important
**Common violations:**
- Using mean with heavily skewed data: Use median instead
- Ignoring outliers when calculating mean: Consider robust alternatives or outlier removal
- Using median when you need mathematical properties: Mean supports algebraic operations better
## 7. Common Mistakes
**Mistake 1: Forgetting to handle missing values**
```r
# Wrong - will return NA
mean(c(1, 2, NA, 4, 5))
```
```
[1] NA
```
```r
# Correct - specify na.rm = TRUE
mean(c(1, 2, NA, 4, 5), na.rm = TRUE)
```
```
[1] 3
```
**Mistake 2: Using mean with highly skewed data**
```r
# Example: Income data with outliers
income <- c(25000, 30000, 35000, 40000, 45000, 1000000)
mean(income) # Misleading due to outlier
```
```
[1] 195833.3
```
```r
median(income) # More representative
```
```
[1] 37500
```
**Mistake 3: Assuming mean and median are always different**
With symmetric distributions, mean and median can be nearly identical, and both provide valid measures of central tendency.
## 8. Related Concepts
**What to learn next:**
- **Mode**: The most frequently occurring value
- **Weighted mean**: When observations have different importance
- **Trimmed mean**: Mean after removing extreme values
- **Geometric mean**: For rates, ratios, and multiplicative processes
- **Standard deviation and variance**: Measures of variability around the mean
**Alternative measures:**
- Use **mode** for categorical data or to find the most common value
- Use **weighted mean** when observations have different sample sizes or importance
- Use **trimmed mean** as a compromise between mean and median
- Consider **quantiles** (quartiles, percentiles) for more detailed distribution analysis
**Advanced applications:**
- **Confidence intervals** around means for inference
- **Hypothesis testing** comparing means between groups
- **Regression analysis** where you predict mean values
- **Time series analysis** using moving averages (rolling means)
Understanding mean and median forms the foundation for more advanced statistical concepts and helps you choose the right measure of central tendency for your specific data and research questions.